テクノロジ系 > 大分類1 基礎理論 > 中分類1 基礎理論 > 1.離散数学 > (4)集合と命題
集合
集合とは、区別できる有限個の要素の集まりです。例えば、犬や猫、日本人、●●株式会社の社員など、区別できるもの(条件が指定できるもの)であればなんでもよく、その条件に当てはまったものを集合と呼びます。
条件によって区別できるということは、真偽を評価できるということです。例えば、犬であるかどうかをtrue(真)、false(偽)で判定できるといったことです。こういった条件を命題と言います。
集合Sの中に要素aがあった場合、S∋a または a∈Sと表します。逆に含まない場合はS∌a または a∉Sと表します。
集合Sの中に要素を全く含まない場合を空集合といい、∅で表します。
部分集合
集合の中に集合が入っている状態を部分集合と言います。
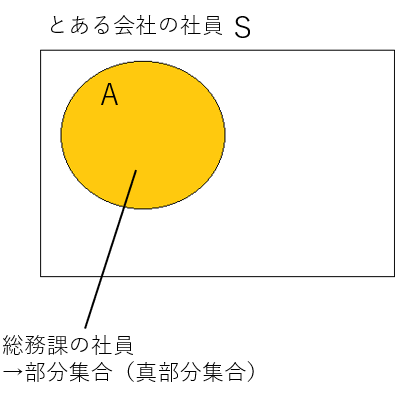
上の図のように、とある会社の社員という集合の中に総務課の社員があったとして、総務課の社員はとある会社の社員にすべて含まれるため、総務課の社員はとある会社の社員の部分集合ということができます。また、このようにとある会社の社員には総務課以外の社員もいる場合、総務課の社員はとある会社の社員の真部分集合ということもできます(例えばとある会社には総務課しかなく全社員が総務課に所属している場合は真部分集合にはなりません)。全体の集合Sの部分集合AをS⊃AまたはA⊂Sのように表します。
集合演算
集合は、2つ以上組み合わせた場合の様々な条件について考えていきます。これを集合演算と言います。集合演算をわかりやすくするツールとしてベン図があります。
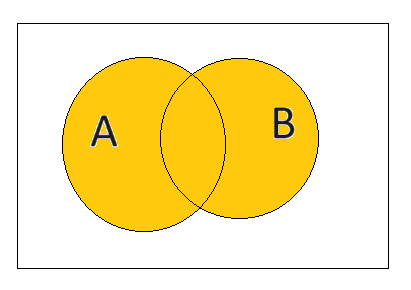
集合演算にはいくつかの種類がありますが、まずは最も基本的な集合演算を5つ解説します。
和集合
二つの集合を足したものです
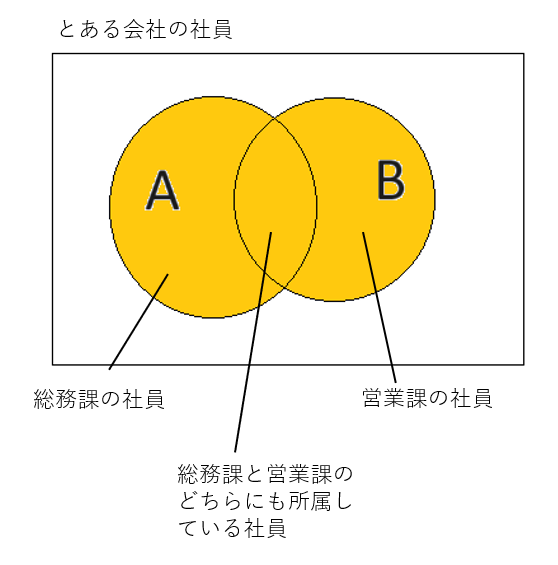
上の図ように、「AまたはB」を表すのが和集合ですが、「どちらにも当てはまる」ものがある場合、単純に足し合わせると誤ります。
以下の表現はすべて和集合を意味します。
- A OR B
- A + B
- A ∪ B
- A ∨ B
積集合
二つの集合の両方に当てはまるものを表すのが積集合です。下のように、「AかつB」を表します。
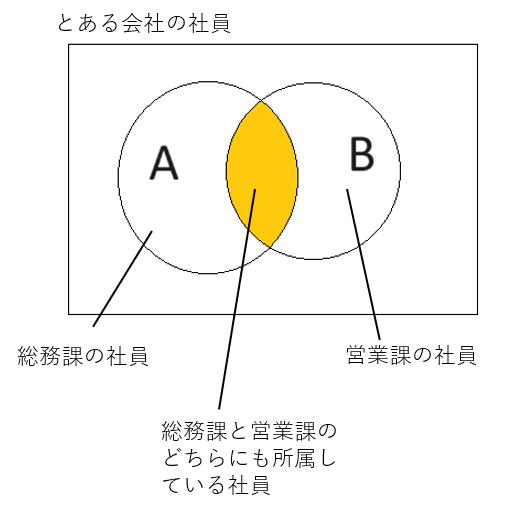
以下の表現はすべて積集合を意味します。
- A AND B
- A ・ B
- A ∩ B
- A ∧ B
補集合
補集合とは集合の否定のことをいいます。
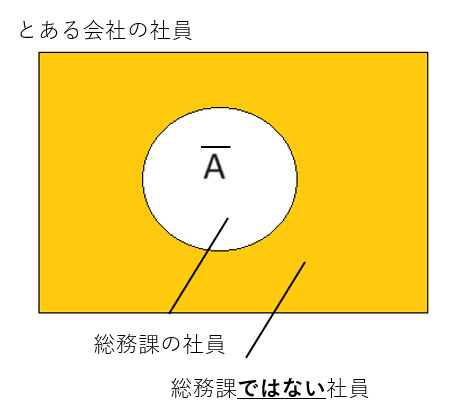
以下の表現はすべて補集合を意味します。
- NOT A
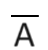
差集合
差集合はある集合から別の集合を引いたものです。
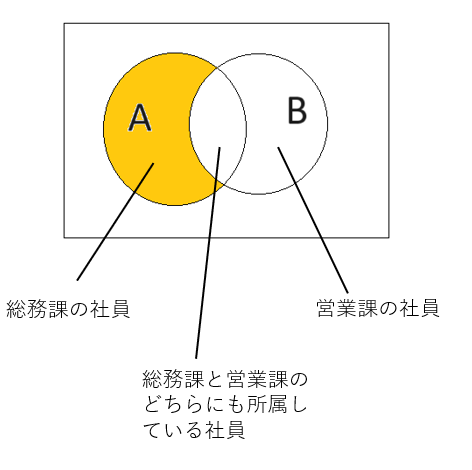
上の図のように、総務課の社員から営業課の社員を引きます。
差集合はA - Bで表されます。
対象差集合
対象差集合は、二つの集合の和集合から両方の条件に当てはまるものを引いたものです。
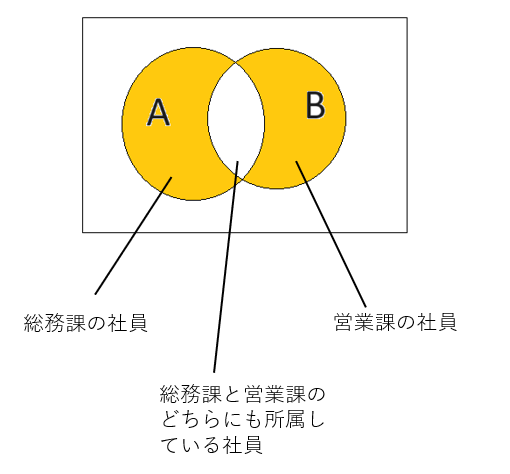
これまでの集合に比べてなじみの薄いものですが、次の章で勉強する論理演算で排他的論理和と呼ばれる重要な概念になります。
以下の表現はすべて排他的論理和を意味します。
- A XOR B
- A ⊕ B
- A △ B


