テクノロジ系 > 大分類1 基礎理論 > 中分類1 基礎理論 > 1.離散数学 > (3)算術演算と精度
2進数の演算
加算
2進数の加算は以下のような筆算を行います。
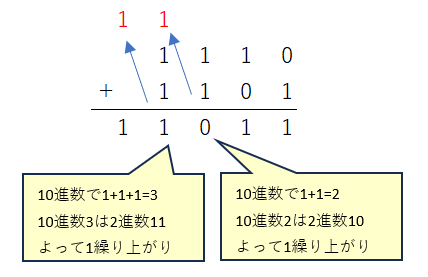
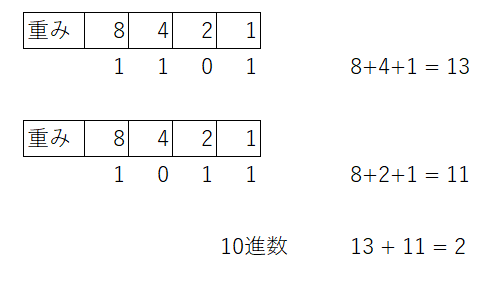
試しに2進数を10進数に直して足し算した結果と、2進数の結果を10進数に直したものを比較すると一致します。
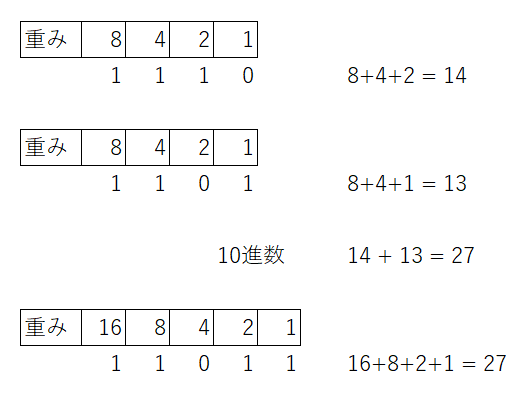
しかし、桁数が4ビットと決まっていた場合は最上位が無視されます。これをオーバーフローと言います。
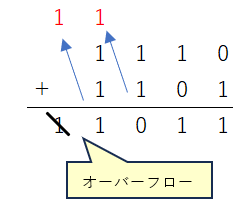
1110+1101は本来であれば11011ですが、オーバーフローが起こると1011になってしまいます。2進数1011を10進数に直すと11なので明らかに正しい計算結果が反映されていないことが分かります。
減算
2進数の減算は以下のように行います。
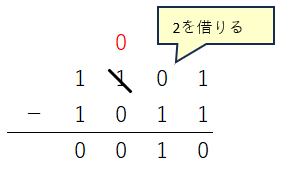
10進数の筆算で引く数が足りなかった場合10を借りてきましたが、2進数の場合は2を借ります。足し算の時と同様に10進数に直して検算をすると一致することが分かります。
シフト演算
シフト演算とはビットを左右にずらす演算のことをいいます。例えば10進数の120という数字を左右にずらしてみます。
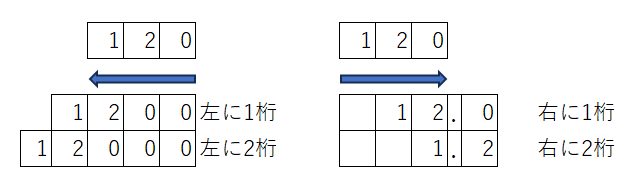
この図からわかる通り、10進数の場合は左に1桁動かすと10倍、2桁動かすと100倍になり、右に1桁動かすと1/10、2桁動かすと1/100になります。
2進数で同様のことをやってみると、左に1桁動かすと2倍、2桁動かすと4倍になり、右に1桁動かすと1/2、2桁動かすと1/4になります。
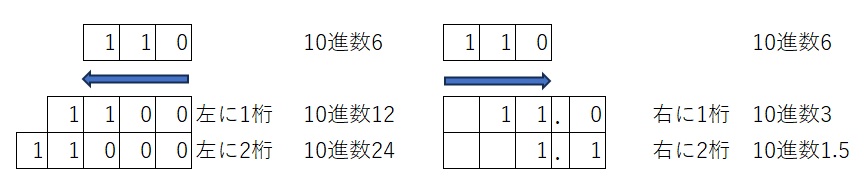
ただし、コンピュータ内部ではビット数(桁数)が決まっているため、決められた桁を超えると無視されます。例えば4ビットだった場合、上の例で左に2桁シフトした11000の最上位の1が無視されて1000になってしまいます。左方向にあふれることをオーバーフロー、右方向にあふれることをアンダーフローと言います。
論理シフトと算術シフト
論理シフトは符号を関係なくずらすことをいい、算術シフトは符号を考慮してずらすことをいいます。
誤差
コンピュータの桁数が有限であることはこれまでも繰り返し述べてきました。例えば10進数では10÷3が3.33333…となり割り切れません。このような数値がある限り、正確な値をコンピュータに持たせることは不可能なので、どうしても誤差が生じます。その誤差の種類についてここで学びます。
丸め
「数を丸める」という表現は普段でも使うことがあるかと思います。この「丸める」とは、例えば5.38792157などという小数点以下にそこそこの数値がある場合に小数第3位を四捨五入して5.39にするといったことを丸めるといいます。丸め方は四捨五入に限らず切り捨て、切り上げなどその時々に応じた丸め方をします。また、丸めることによって生じた誤差を丸め誤差といいます。
打切り
丸めとよく似ているのが打切りです。打切りとは、10÷3の計算結果が3.3333…となって割り切れないときに、その計算結果を途中で止めることをいいます。打切りによって生じる誤差を打切り誤差といいます。
桁落ち
ほぼ等しい二つの数値の減算を行った際に有効桁数が減ってしまうことによって生じる誤差です。

有効桁数とは意味のある桁、信頼できる桁という意味です。上の例の場合、1.22223は有効桁ですが、減算後は浮動小数点数表現を行うために正規化が行われ、1の部分のみが有効桁になります。
減算前の数値1.22223と1.22222は、表示されている桁の数は有効ですがその下に実はもともと別の数値がある可能性があった場合に誤差が発生します。

この例の場合、実際の計算結果は0.000014512になりますが、その結果が反映されていません。本来であれば1.4512×10の-5乗のような数値になるところを0で埋められて1.0000×-5乗のような数値になっていることになります。桁落ちが発生した演算の後にさらに計算が続いた場合に誤差が増大していきます。
この誤差は桁数が有限である以上避けられないものですが、なるべく避ける方法として桁落ちが発生しそうな近い数の減算は後回しにするという方法があります。
情報落ち
絶対値が大きい数値と非常に小さい数値の加減算を行ったときに、非常に小さい値が計算結果に反映されないことを情報落ちと言います。

例えば桁数が6桁までと決まっていた場合、上のように計算した場合0.0023の23の部分が入りきらずに情報落ちが発生します。


