テクノロジ系 > 大分類1 基礎理論 > 中分類1 基礎理論 > 1.離散数学 > (1) 基数
この章では基数の基本的な事柄について学びます。
(1)基数
基数(radix)とは、何種類の記号を使用して数値を表すかを示す数です。一般的に「r進数」と呼んだ場合のrが基数となります。
例えば、普段私たちが使っている数値表現は10進数です。これは0~9までの10個の記号(数字)で数値を表し、基数は10です。
コンピュータの世界では2進数が用いられます。これは0と1の2つの記号で数値を表し、基数は2です。また、2進数と相性が良いことからコンピュータの世界では8進数と16進数が良く用いられます。8進数は0~7の8個の記号で数値を表し基数は8、16進数は0~9とA,B,C,D,E,Fの16個の記号で数値をで表し、基数は16です。
基数による数値の表し方はは無数にありますが、コンピュータでよく扱うのが2進数、8進数、16進数と普段私たちが使っている10進数です。基本的にはこの4つについての表現方法を覚え、相互変換ができるようになっておきましょう。特に2進数は重要で、ネットワーク分野のIPアドレスでは分からないと問題が解けません。しっかりと理解しておきましょう。
10進数、2進数、8進数、16進数
10進数、2進数、8進数、16進数の対応は以下の表の通りになっています。
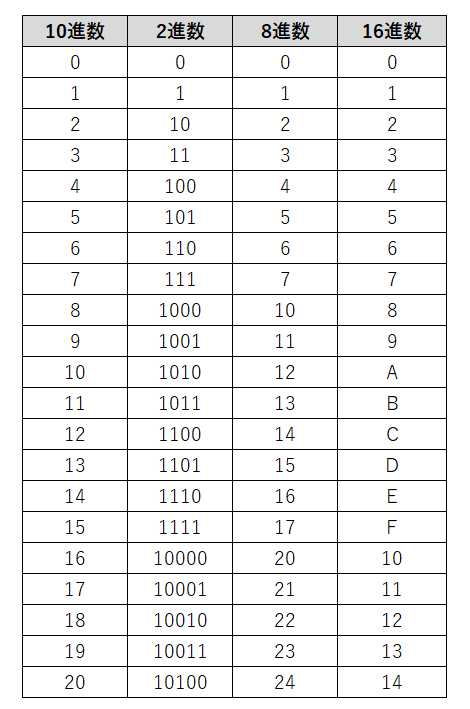
この表を使えば例えば10進数→2進数のように変換することが可能です。しかし、10進数100のような数値の変換をする場合にはそれなりの大きな表を持っていないといけないですし、本試験の時に表を書き出すのは現実的ではないです。よって、表を用いないで相互変換ができるように練習しておく必要があります。この章では桁の重みについて学んだあと、最も大事な10進数と2進数の相互変換を学び、その知識を基にそのほかの相互変換もできるように練習します。
桁の重みと重み表
桁の重みとは、各桁の単位のことをいいます。
例えば10進数の場合は1の位、10の位、100の位と言いますが、この「位」にあたる数のことが桁の重みです。そして1、10、100という数値はそれぞれ基数である10の0乗、1乗、2乗になっています。

重みを一覧にしたものを重み表といいます。10進数の重み表は以下の通りです。
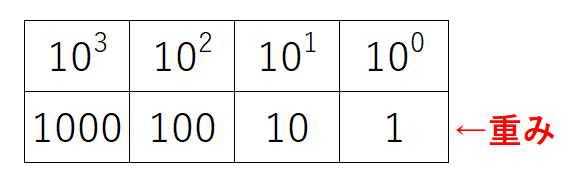
2進数の場合は基数である2を累乗していくことにより重みを計算できます。2進数の重み表は以下の通りです。
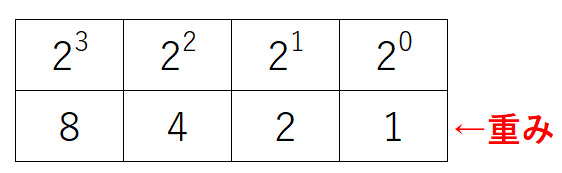
8進数や16進数も同様に重み表を作成することができます。
重み表を使用するとr進数⇔10進数の基数変換を行うことができます。具体的な手順は次で解説します。
基数変換
r進数⇔10進数の相互変換
r進数⇔10進数の相互変換は重み表を使って変換します。
2進数→10進数
2進数10010を10進数に変換してみることで手順を示します。
① 2進数の重み表を作成する。
2進数の桁数によって表の大きさは異なりますが、今回は5桁分の重み表を書き出します。
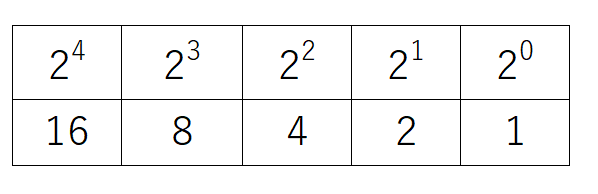
② 作成した重み表の下に2進数の数値を書き込む。
一つの重みに対して一つずつ2進数を書き出します。
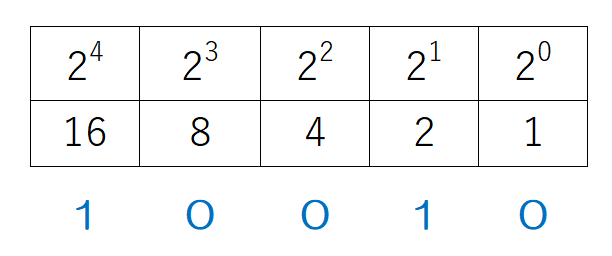
③ 重み×2進数の桁の掛け算をする
重みの値と2進数の桁の値を掛け合わせ、その下に書き出します。2進数は0と1しかないため、実際には2進数で1の桁のところ重みがそのまま下に書き出される形になります。
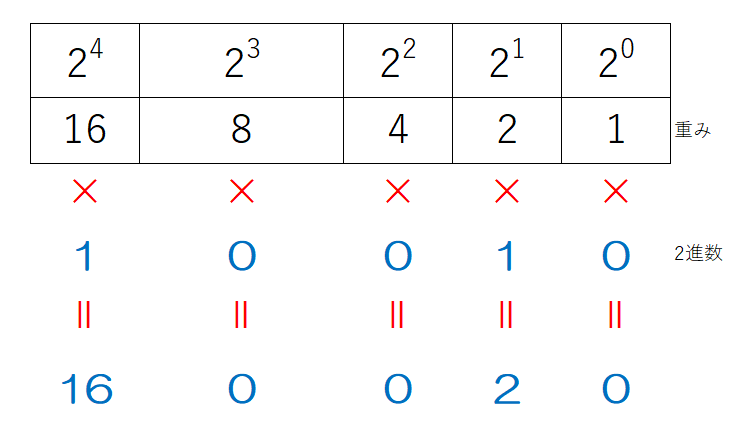
④ ③で書き出した値をすべて足し算する
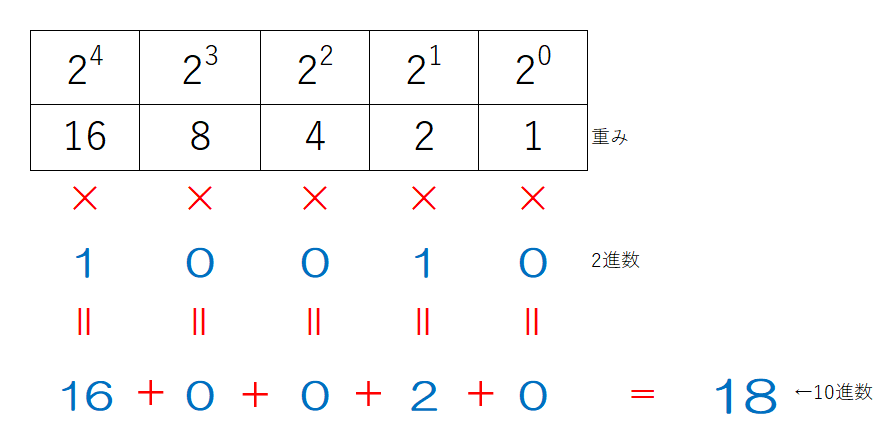
10進数→2進数
先ほど変換した10進数18を今度は2進数に戻してみましょう。
① 2進数の重み表を作成する
重み表のサイズはこの後の②によって変わります。

② 重み ≦ 10進数の数値 となるもののうち、重みが最大のものを探して、その重みの下に10進数の数値を書き込む
ここは少し手順が難しいです。下の図のように考えて適切な位置に10進数の数値を書き込みます。

③ 10進数の数値÷重みの計算を行い、商を10進数の数値の下に、あまりを10進数の数値の右側の重みの下に書き込む
2進数の場合は商は必ず1になり、あまりは「10進数の数値-重み」になります。しかし、他の基数で応用するために「10進数の数値÷重み」の商とあまりであることは覚えておきましょう。
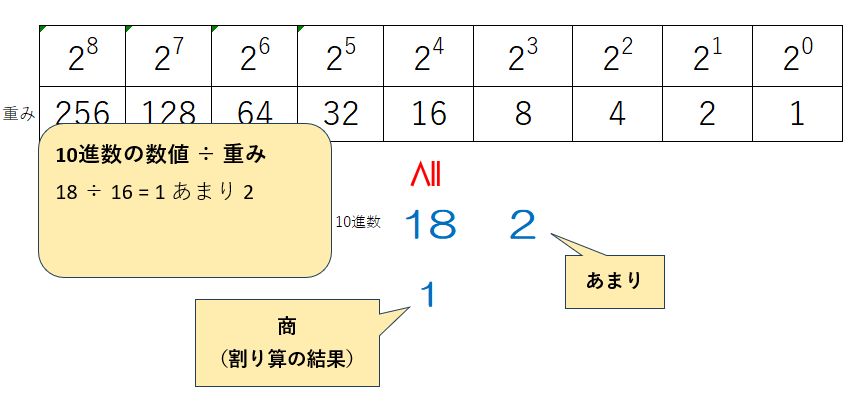
④ ③で書き込んだあまりの値について、重み ≦ あまりの数値となるもののうち、重みが最大のものを探して、その重みの下にあまりの数値を書き込む
③で書いたあまりの値について②と同じようなことをします。これも手順が少し難しいため練習が必要です。

⑤ ④で書き込んだあまりの値 ÷ 重みの計算を行い、商をあまりの下、あまりを右側の重みの下に書き込む
③と同様の手順となります。
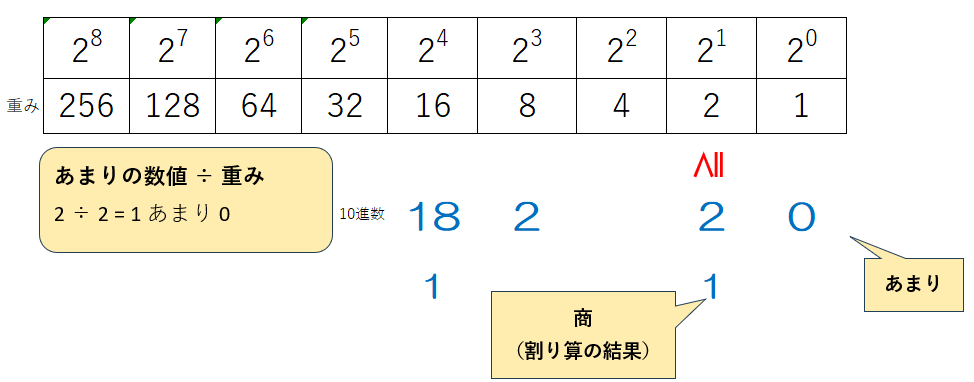
⑥ ④⑤をあまりが0になるまで繰り返す
この例では既に余りが0になったのでここで終了です。
⑦ 商を書き込んだ列で空白になっているところを0で埋めると2進数に変換されている
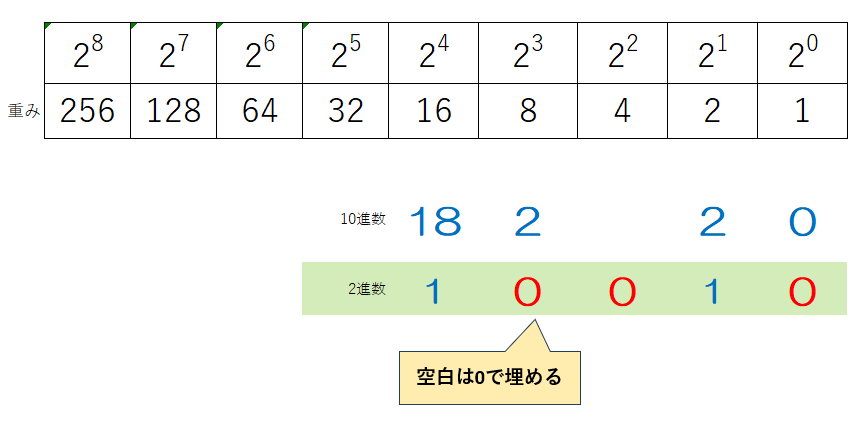
10進数→2進数(別解)
10進数→2進数変換は以下のような筆算で割り算の結果と余りの値を書き、最後に下からあまりの値を拾っていくような方法が知られています。
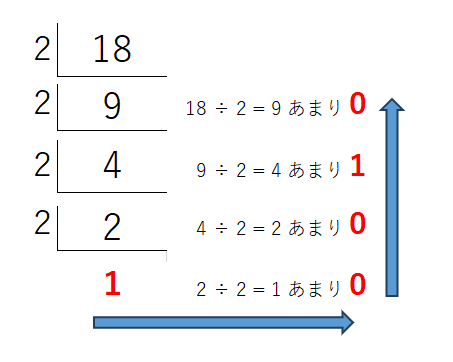
8進数→10進数
8進数→10進数も2進数と同じ手順で変換できます。詳細な解説は省きますが、例えば8進数2475を10進数に変換すると以下のようになります。
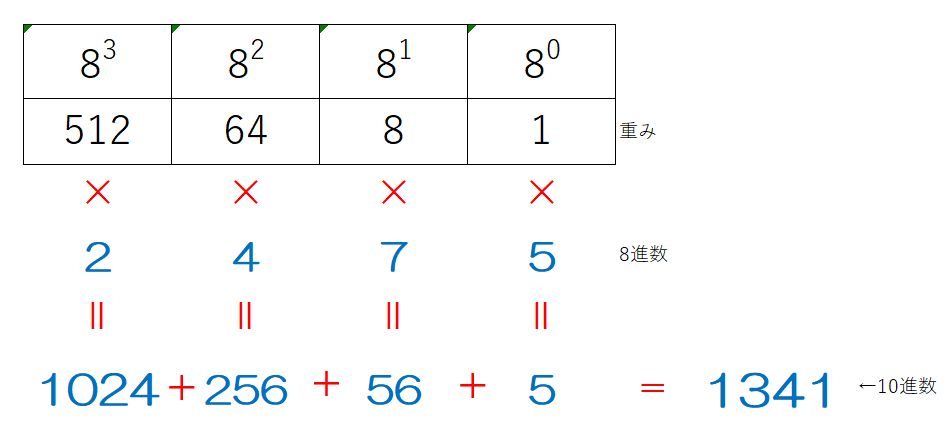
10進数→8進数
10進数→8進数の変換も重み表を用いて、2進数の時と同じように計算します。ただし数が大きくなっているため計算が面倒です。変換する機会は2進数ほど多くありませんが、2進数以外の変換も出題されることがあるため方法を把握しておきましょう。
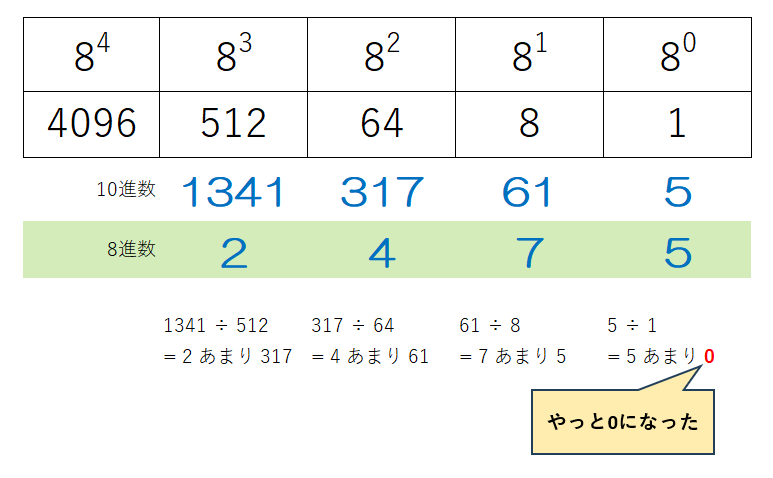
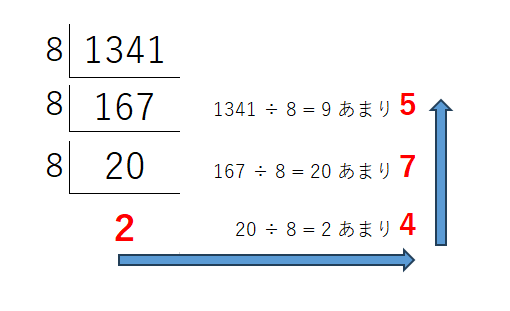
10進数→8進数(別解)
別解による方法も2進数と同じように変換できます。割るときの値が8進数の基数である8になりますが、あまりを拾っていくところは同様です。
2進数⇔16進数
2進数→16進数、16進数→2進数の変換も同じようにできます。ここでは解説を省きます。
r進数⇔2進数の相互変換
r進数⇔2進数の相互変換は10進数のほかは8進数、16進数ができるようになっているとよいです。特に16進数は重要です。といっても2進数⇔10進数との相互変換が分かっていれば難しくはありません。
2進数→8進数
2進数10011を8進数にしてみます。
① 2進数を3桁ずつ分ける
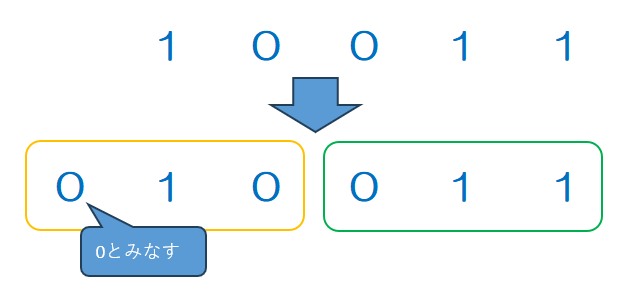
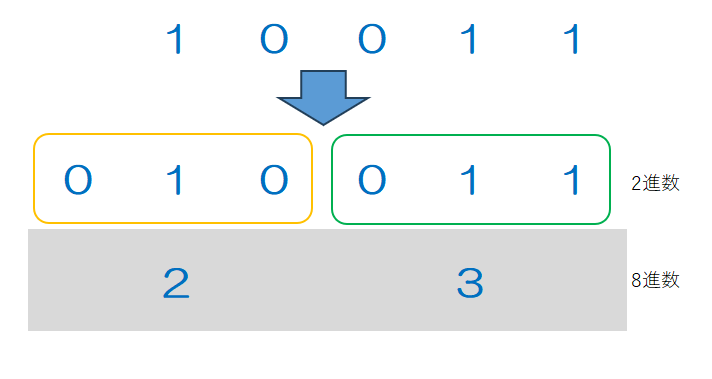
② 分けたそれぞれのブロックを8進数に直して結合すると8進数になる
2進数⇔10進数の変換が身についていると変換は容易です。よくわからない場合は2進数⇔10進数変換を良く練習しましょう。
2進数10011を8進数にすると23になります。
8進数→2進数
2進数→8進数と逆のことをすればいいので詳細は省きます。8進数23を2進数010011に直してみましょう。
2進数→16進数
2進数10101000を16進数にしてみます。
① 2進数を4桁ずつ分ける
8進数では3桁ずつですが、16進数では4桁ずつです。今回の例では関係ないですが、上の桁が足りない場合その桁を0とみなすのは8進数と同様です。
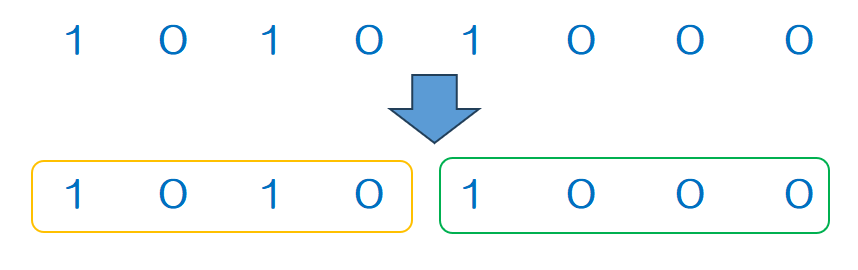
② 分けたそれぞれのブロックを16進数に直して結合すると16進数になる
2進数⇔10進数の変換が身についていると変換は容易です。よくわからない場合は2進数⇔10進数変換を良く練習しましょう。
2進数10101000を16進数にするとA8になります。
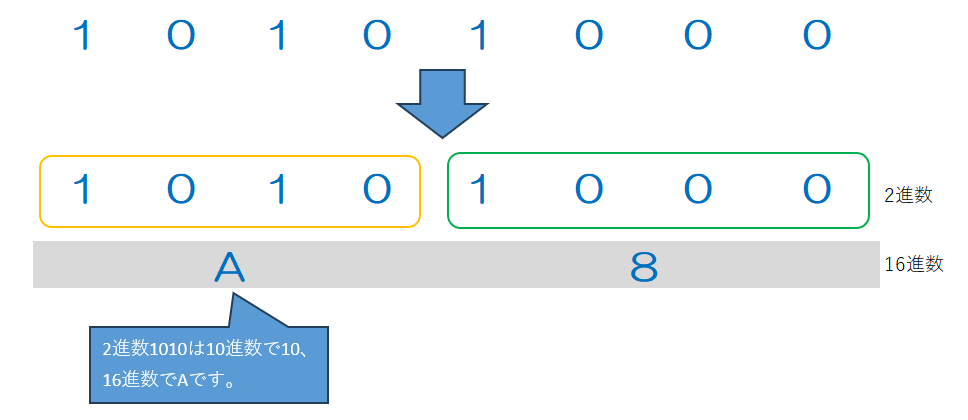
例えば、16進数のA8を変換したい場合、Aと8に分解し、それぞれ10進数変換を経て2進数に変換します。その後それをつなげると全体の2進数に変換できます。
16進数→2進数
2進数→16進数と逆のことをすればいいので詳細は省きます。8進数A8を2進数10101000に直してみましょう。
過去問演習
基数は情報処理試験においては基本中の基本なので、応用情報技術者試験においては応用的な難しい問題が出題される傾向にあります。これらの問題が答えを見てもわからない場合は基本情報やITパスポートの問題を解いてみることをお勧めします。
問1
0以上255以下の整数nに対して,
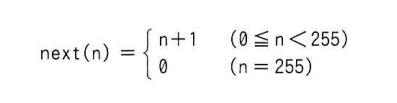
と定義する。next(n)と等しい式はどれか。ここで,x AND y 及び x OR y は,それぞれxとyを2進数表現にして,桁ごとの論理積及び論理和をとったものとする。
イ.(n+1) AND 256
ウ.(n+1) OR 255
解答:ア
2進数の応用問題です。過去何回も出題されている定番の問題なので、答えるようになっておきたいです。
式は「nが0以上255未満の時n+1になり、nが255の時は0になる」という意味です。例えば、nが254だった場合は計算結果が255になり、nが255だった場合は計算結果が0になります。
これが成り立つものを、ア~エの選択肢一つ一つに対して計算を行ってみることで解答を導きます。

【出題歴】
- 令和5年春期 問1
- 平成31年春期 問1
- 平成27年秋期 問1
- 平成22年春期 問1



