テクノロジ系 > 大分類1 基礎理論 > 中分類1 基礎理論 > 2.応用数学 > (6)待ち行列理論
待ち行列理論とは、利用者が窓口に行列するようなときの混雑現象を解析する理論のことを言います。待ち行列理論には理論的に様々なものが存在しますが、応用情報技術者試験に出題されるのは現在のところM/M/1モデルに限定されています。
M/M/1モデル
M/M/1モデルは、待ち行列モデルの中で最も基本的なもので、応用情報技術者試験でも頻出です。以下の条件を持つ待ち行列を分析します。
- 窓口は一つのみである
- 窓口にやってくる利用者がやってくる時間間隔は、ポアソン分布に従いランダムである
- 利用者が窓口でかかる時間の長さは、指数分布に従いランダムである
これらの条件下であると仮定した場合の、以下の3つの事柄について分析します。
2つの指標 λ、μ
①平均到着率 λ(ラムダ)
一定の時間あたりに窓口に到着する人数です。
例えば、1時間あたり16人到着する場合、平均到着率λは16人/時間。
平均してどのくらいの時間間隔で窓口に利用者が到着するかという指標を平均到着時間 Taと言い、平均到着率λの逆数(1/λ)となる。平均到着率λが16人/時間の場合、平均到着時間Taは1/16時間=3分45秒となる。
②平均サービス率 μ(ミュー)
窓口が一定の時間当たりに何人分の処理ができるかを表す指標。
例えば、1時間あたり20人処理できる場合、平均サービス率μは20人/時間。
窓口の処理時間が平均してどのくらいかという指標を平均サービス時間 Tsと言い、平均サービス率μの逆数(1/μ)となる。平均サービス率μが10人/時間の場合、1/20時間=3分となる。
③平均利用率ρ(ロー)
窓口の混雑度合いを表す指標。
2つの公式
覚えておきたい公式は2つあります。
公式1平均利用率ρ(ロー)を求める公式
平均利用率ρ(ロー)は窓口の混雑度合いを表す指標です。これは平均到着時間と平均サービス率から求めます。
$$平均利用率 ρ=\frac{平均到着率 λ}{平均サービス率 μ}$$
つまり、到着する人数を処理できる人数で割った数が平均利用率になります。
平均到着率λは16人/時間、平均サービス率μは20人/時間の例では、16 ÷ 20 = 80%になります。
公式2平均待ち時間Twを求める公式
平均待ち時間Twは窓口でどれだけ待たされるかを表す指標です。これは平均利用率と平均サービス時間から求められます。
$$平均待ち時間Tw =\frac{ 平均利用率ρ }{1–平均利用率ρ} \times平均サービス時間Ts$$
利用率80%、平均サービス時間1/20時間(3分)の例では、0.2時間(12分)になります。
公式2によると、平均利用率が50%(0.5)の時に$$平均待ち時間Tw = 平均サービス時間Ts$$となります。一度公式に当てはめて計算してみるとよいでしょう。この論点は応用情報技術者試験で何度か問われています。
過去問① 令和4年春期 問3
M/M/1の待ち行列モデルにおいて,窓口の利用率が25%から40%に増えると,平均待ち時間は何倍になるか。
ア.1.25
イ.1.60
ウ.2.00
エ.3.00
解答:ウ
利用率とは平均利用率ρのことで、公式2を使用して解答を導くことができます。
利用率が25%(0.25)の時:
$$\frac{0.25}{1-0.25}×Ts = \frac{1}{3}× Ts$$
よって、
$$平均待ち時間Tw=\frac{1}{3}× Ts$$
利用率が40%(0.4)の時:
$$\frac{0.4}{1-0.4}×Ts = \frac{2}{3}× Ts$$
よって、
$$平均待ち時間Tw=\frac{2}{3}× Ts$$
以上から、平均待ち時間は利用率40%の時は利用率25%の時の2倍となっていることが分かります。よって解答はウです。
過去問② 令和3年秋期 問2、平成27年春期 問1
ATM(現金自動預払機)が1台ずつ設置してある二つの支店を統合し,統合後の支店にはATMを1台設置する。統合後のATMの平均待ち時間を求める式はどれか。ここで,待ち時間はM/M/1の待ち行列モデルに従い,平均待ち時間にはサービス時間を含まず,ATMを1台に統合しても十分に処理できるものとする。
〔条件〕
・平均サービス時間:Ts
・統合前のシステムの利用率:両支店ともρ
・統合後の利用者数は,統合前の両支店の利用者数の合計
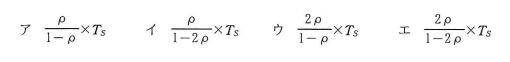
解答:エ
平均サービス時間は「窓口の処理時間が平均してどのくらいか」という指標であり、本問においてはシステムの性能に関わってきます。統合したとしてもシステム性能は変わらないことから平均サービス時間Tsは変わりません。利用率ρは統合したことによって2店舗の利用率を足し合わせた数値になることが考えられることから、統合後は2ρとなります。
よって、ρを適切に2倍しているエが正解となります。
過去問③ 令和元年秋期 問3、平成25年秋期 問5、平成21年春期 問1
通信回線を使用したデータ伝送システムにM/M/1の待ち行列モデルを適用すると,平均回線待ち時間,平均伝送時間,回線利用率の関係は,次の式で表すことができる。

回線利用率が0から徐々に増加していく場合,平均回線待ち時間が平均伝送時間よりも最初に長くなるのは,回線利用率が幾つを超えたときか。
ア.0.4
イ.0.5
ウ.0.6
エ.0.7
解答:イ
公式2の解説にある通り、平均利用率が0.5の時に平均待ち時間 = 平均サービス時間になります。本問においては平均利用率→回線利用率、平均待ち時間→回線待ち時間、平均サービス時間→平均伝送時間となっていますが、公式については同じです。よって、平均利用率が0.5を超えたときに平均伝送時間が長くなっていくことから、イが正解です。
過去問④ 平成30年秋期 問2、平成26年秋期 問3
コンピュータによる伝票処理システムがある。このシステムは,伝票データをためる待ち行列をもち,M/M/1の待ち行列モデルが適用できるものとする。平均待ち時間がT秒以上となるのは,処理装置の利用率が少なくとも何%以上となったときか。ここで,伝票データをためる待ち行列の特徴は次のとおりである。
・伝票データは,ポアソン分布に従って到着する。
・伝票データをためる数に制限はない。
・1件の伝票データの処理時間は,平均T秒の指数分布に従う。
ア.33
イ.50
ウ.67
エ.80
解答:イ
問い方が異なりますが過去問③と同じ趣旨の問題です。「平均待ち時間がT秒以上となるのは」と問われていますが、下に挙げられている特徴に「1件の伝票データの処理時間は,平均T秒の指数分布に従う。」とあることから、平均待ち時間≧平均処理時間(平均サービス時間のことです)となる値を求めればよいことになります。公式2の解説にある通り、平均待ち時間=平均サービス時間になるのは50%の時なので、イが正解です。
M/M/1モデルのポイント
M/M/1モデルは応用情報技術者試験で頻出で、用語と公式は正確に覚える必要があります。また、数学が苦手な場合は時間⇔分の相互変換や、分数・小数の計算に苦労すると思います。そのため例題を利用して計算練習をする必要があります。
ただし過去問の出題の種類は限られており、過去に出題された同じ問題が繰り返し出題される傾向にあります。そのため、時間がない場合は過去問に出題されたものは少なくとも解けるように対策をしておけるとよいでしょう。

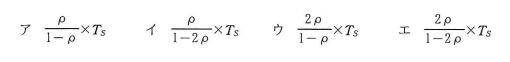


ポアソン分布、指数分布の深い理論的なところまでわからなくても過去問レベルではOKです。一定ではなくランダムでやってくるんだなというところを押さえておきます。