論理演算

テクノロジ系 > 大分類1 基礎理論 > 中分類1 基礎理論 > 1.離散数学 > （5）論理演算

論理式と論理演算

論理式とは命題を論理記号を用いて表した式であり、論理式で表される演算を論理演算と言います。コンピュータの内部では数式による演算の他に論理式による論理演算も行われています。論理演算は前の章で勉強した集合演算をコンピュータ用に置き換えたものとみることもでき、同じようにベン図を用いて表現できます。また、真理値表という1（真・True）と0（偽・False）の組み合わせ表を使って表すこともできます。

基本の論理演算

基本の論理演算としては、論理和、論理積、否定、排他的論理和、否定論理和、否定論理積があります。

論理和

論理和は集合演算の和集合と同じです。和集合と同じく以下の記号で表します。

• A OR B
• A ＋ B
• A ∪ B
• A ∨ B

ベン図で表すと以下のようになります。

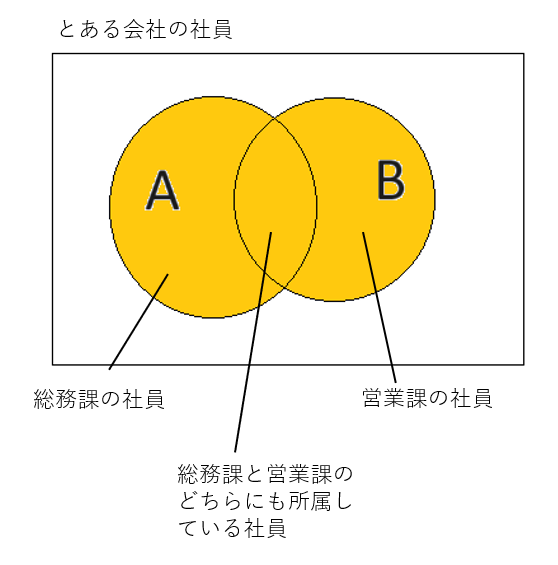
真理値表は以下の通りです。

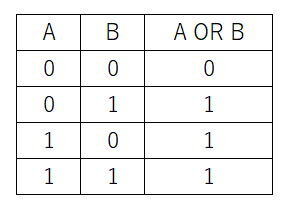
論理積

論理積は集合演算の積集合と同じです。積集合と同じく以下の記号で表します。

• A AND B
• A ・ B
• A ∩ B
• A ∧ B

ベン図で表すと以下のようになります。

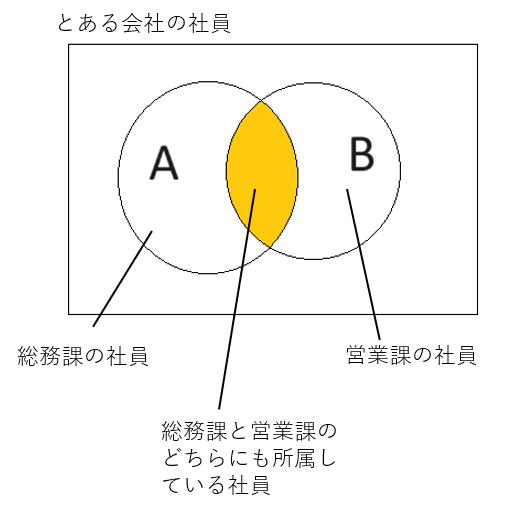
真理値表は以下の通りです。

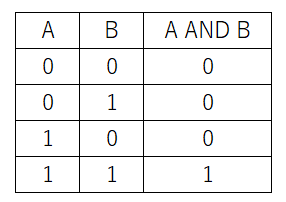
否定

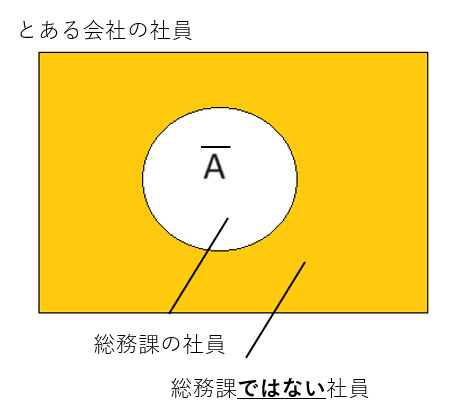
否定は集合演算の補集合と同じです。補集合と同じく以下の記号で表します。

• NOT A
• 

ベン図で表すと以下のようになります。

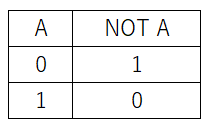
真理値表は以下の通りです。

排他的論理和

排他的論理和は集合演算の対象差集合と同じです。対象差集合と同じく以下の記号で表します。

• A XOR B
• A ⊕ B
• A △ B

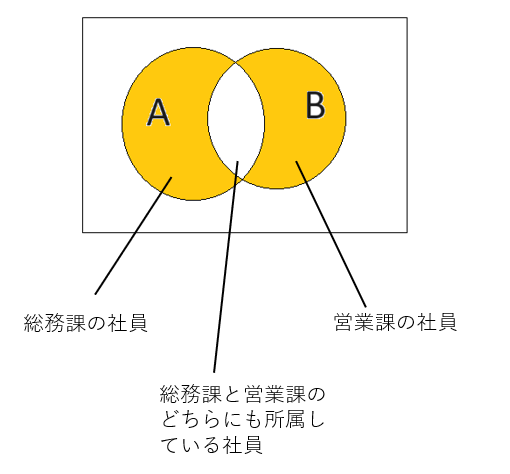
真理値表は以下の通りです。

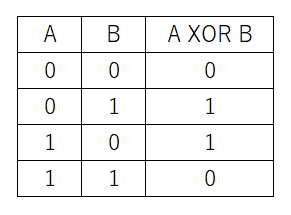
否定論理和

否定論理和は論理和の結果を反転したものです。NORで表します。

真理値表は以下の通りです。

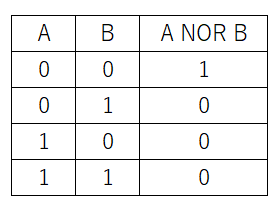
否定論理積

否定論理積は論理積の結果を反転させたものです。NANDで表します。

真理値表は以下の通りです。

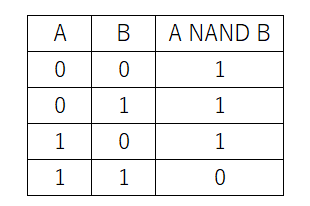
論理演算の基本法則

論理式は法則を使って変形をすることによって簡略化をします。有名な法則としては、結合の法則、分配の法則、ド・モルガンの法則

結合の法則

演算の順番を変えても結果が変わらないという法則を結合の法則と言います。

論理和
(A ∪ B) ∪ C = A ∪ (B ∪ C)

論理積
(A ∩ B) ∩ C = A ∩ (B ∩ C)

排他的論理和
(A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)

分配の法則

括弧内の演算を括弧の外に分配して演算する法則を分配の法則と言います。

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

ド・モルガンの法則

ド・モルガンの法則は論理和、論理積とその否定に成り立つ法則です。

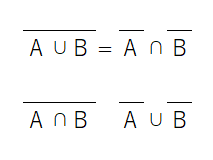
カルノー図

カルノー図とは論理式を簡略化するための手法です。例えば以下の図を論理変数としたときに、A～Dを用いて論理式に表します。

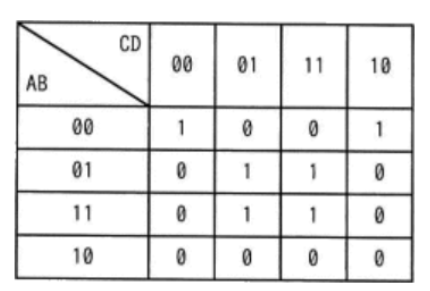
まずは、以下のようにしてグループ化を行います。

１．1が記入されているセルをグループ化する。<2>２．グループ化するセルは2ⁿ個とする。
３．カルノー図の上下左右は連続していると考える。

この法則に従ってグループ化すると、以下の図のように黄色と青のグループができます。

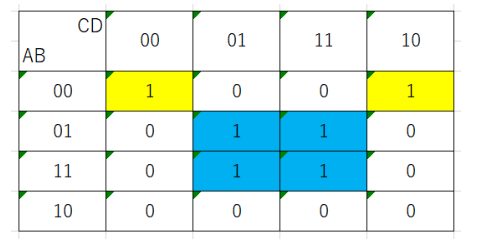
次に、このグループを論理式に変換します。
黄色のグループの左側の1は、右側の1は、青のグループは左上からそれぞれ、とあらわすことができます。黄色のグループで共通するのは、青のグループで共通するのはBDであり、グループ内で論理積を取り、グループとグループで論理和をとることで論理式を導くことができます。よってと表されます。