テクノロジ系 > 大分類1 基礎理論 > 中分類1 基礎理論 > 1.離散数学 > (2) 数値の表現
基数の章では正の整数に限り取り扱いました。この章ではマイナスや小数点といった正の整数以外の表現方法について取り上げます。
負の数の表現
負の数とはマイナスの数です。基数の章では正の数しか取り扱いませんでした。ここでは負の数をどう表現するかについて解説します。
表現の方法はいくつかありますが、ここでは「符号+絶対値方式」と「2の補数」の2つの方式について解説します。
符号+絶対値で表す方式
符号+絶対値で表す方式は、負の数を扱うための最も単純な方法です。その名の通り、先頭にプラスかマイナスの符号を付ける方式で、普段私たちが10進数でマイナスを扱う際も-3のように表現すると思います。
しかし、コンピュータ内部では必ず2進数で数を扱い、+-のような符号も用いることができません。そこで通常、先頭1ビットについて正の数が0、負の数が1と決めて表現します。例えば01は+1、11は-1となります。
普段使っている表現通りなので人間にとってはわかりやすい表現と言えますが、次のデメリットがあります。
- 0の表し方が2通りある
0の表現方法は00と10の二通りあります。同じ数値なのに2通り表現方法があると、コンピュータで数値を扱うときに処理が煩雑になることがあります。 - 計算が煩雑になる
加算・減算などの計算が、次に示す2の補数より煩雑になります。
これらのデメリットがあるため、コンピュータでよく使われるのは2の補数で表す方式です。
2の補数で表す方式
現在コンピュータで広く使われている負の数の表現方法が2の補数です。
2の補数とは、2進数においてある数について足すと1桁多くなる最小の数のことをいいます。n桁の2進数、ある数をxとすると以下の数式で表されます。
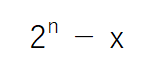
例えば、3桁2進数の011(10進数3)の2の補数は、次のように計算されます。
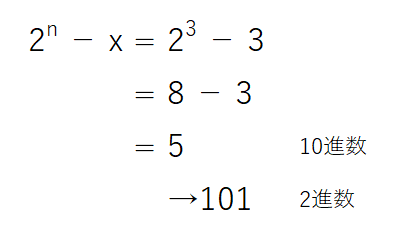
これは2進数で足すと1桁多くなる最小の数になっています。
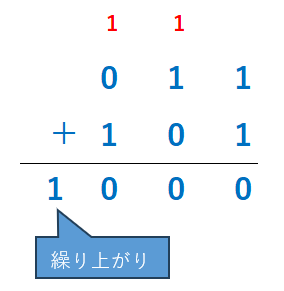
3桁の2進数で表せる数を一覧にすると以下のようになります。
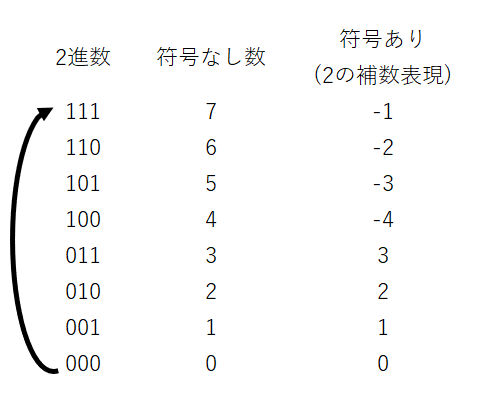
このように、3桁の2進数は符号なし数では0~7を表せますが、符号あり数(2の補数表現)では-4~3までの数を表すことができます。また、先頭1ビットが0の場合は正の数、1の場合は負の数を表しているため、符号+絶対値で表す方式とも親和性が高いです。
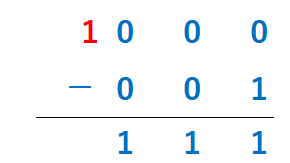
左にある矢印ですが、これは2進数000から1を引いた数が111となり、これを-1としていることを表しています。000から1を引くときに、仮に先頭に1がついていて1000とすることにより無理やり引くと111になります。
2の補数表現の基本的な考えは以上ですが、実際に2の補数を求めるときの手順や表せる範囲について以下で詳しく見ていきます。
【参考】
京都産業大学 「負数の扱い」
https://www.cc.kyoto-su.ac.jp/~kbys/kiso/number/negative.html
2の補数の求め方
2進数の2の補数は、ある数の0と1を反転(符号反転と呼びます)させて1を足す方法により、容易に求められます。例えば、3ビットの2進数011では次のように求めます。
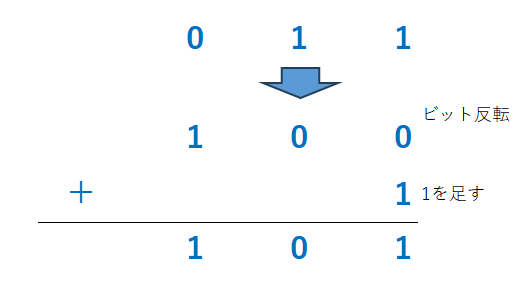
つまり、2進数の2の補数を負の数としたときに、ある数の負の数を求めたい場合はこの操作を行えば求めることができることになります。
表せる範囲
負の数を2の補数で表す形式の場合、n桁で表現できる範囲は以下の通りです。
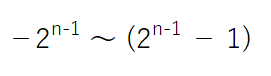
例えば、8桁の場合は以下のように計算できるため、-128~127になります。
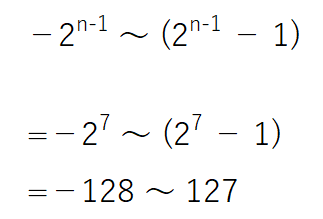
負の数の方が1つ多く数を表せるのはゼロを正の数で使っているからです。
小数の表現
ここまでは正負の整数について勉強してきました。ここからは小数点以下の値について勉強していきます。小数は12.345の345が小数となり、ドットより右側の値として表現します。2進数においても1010.001のように表現します。
小数において重要なのはかなり小さい値(例:0.0000001)や割り切れない値(例:1/3は0.33333…です)の存在です。コンピュータは8桁や16桁のように有限の桁で表現するため正確に表現することは難しく、近似値として表現せざるを得ず誤差が生じます。この問題の処理が大きな課題となります。
小数の表現方式として大きく固定小数点数と浮動小数点数があります。それぞれについて解説します。
固定小数点数
固定小数点数とは文字通り小数点の位置が決まっている小数の表現方式です。8ビットの2進数では例えば1010.0010のように「4ビットずつに分ける」と決めておく方式をいいます。この方式は見た目にはわかりやすいですが、表現できる幅が決まってしまっているため、例えば0000.0000000001011のような値を表現する場合、0000.0000になってしまうなど誤差が生じやすい方式です。そのため、一般的には次に解説する浮動小数点数を使用します。
浮動小数点数
浮動小数点とは文字通り小数点が動く表現方式です。例えば10進数の12.345という数値は以下の計算式の結果と同じ値です。
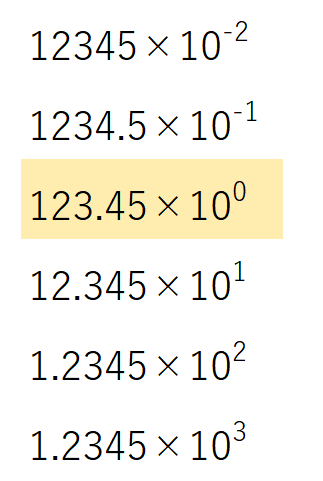
この仕組みを使うと小数点を動かして数値を表現することが可能です。これを規格化したのがIEEE754フォーマットです。この規格の形式はいくつかの種類が存在しますが、応用情報技術者試験のシラバスでは単精度浮動小数点数と倍精度浮動小数点数の2種類が用語例として挙げられています。
単精度浮動小数点数
IEEE754の単精度浮動小数点数と呼ばれる方式は32ビットの2進数で表す方式で、以下のフォーマットになっています。

そして、実際の数値としては以下の式で求められます。
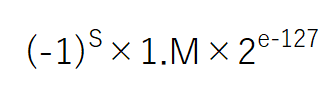
S 符号部:1ビット
浮動小数点数の場合は符号で正負を表す方式となっており、0が正、1が負を示します。-1の0乗は1であり、-1の1乗は1となるため計算式に当てはめると正負が決まります。
E 指数部:8ビット
10進数では10の指数で表しましたが、2進数では2の指数で表現します。IEEE754では指数部の値を正の数で表現するためにバイアス値を引くことで指数部を表現します。単精度浮動小数点数の場合は127になります。これを下駄ばき表現と呼びます。
M 仮数部:23ビット
例えば、2進数の00111110001000000000000000000000という数値があった場合、次のようにフォーマットに当てはめて計算します。

この計算により、2進数00111110001000000000000000000000は10進数0.15625であることがわかります。
倍精度浮動小数点数
単精度浮動小数点数が32ビットで表すのに対し、倍精度浮動小数点数はその倍の64ビットで表します。基本的な考え方は単精度の場合と同じですが、各部のビット数やバイアス値が異なります。
S 符号部:1ビット
単精度と同じです。
E 指数部:11ビット
バイアス値は1023です。
M 仮数部:23ビット
【補足】小数点以下の2進数
小数点以下の2進数について、10進数との相互変換の扱いを中心に補足をします。
2進数→10進数
小数点以下を含めた場合の重み表は以下になります。これを用いると、小数点以下を含めた場合の2進数を10進数に変換できます。

例えば、1101.011を10進数に変換します
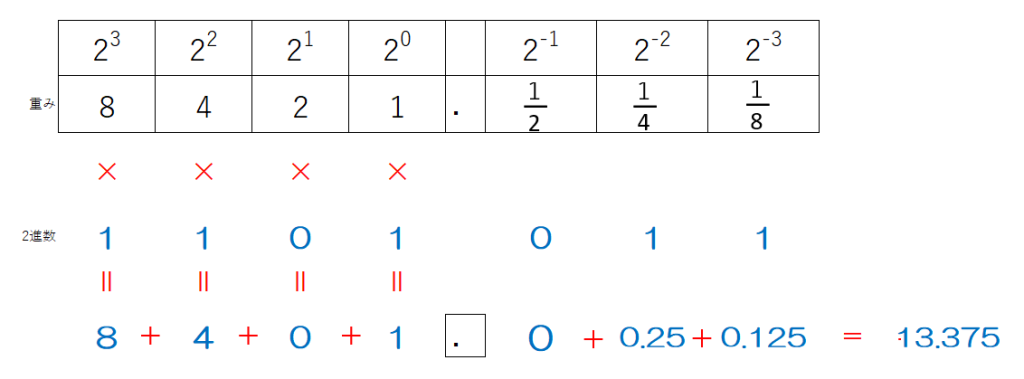
10進数→2進数
10進数→2進数の変換で小数点以下がある場合は、整数部と小数部で分けて変換します。整数部については上で説明した通りなので省きます。
例えば、先ほどの10進数13.375を2進数に変換します。13の部分は1101になります。
小数部の0.375は次のように乗算していき、整数部を拾います。
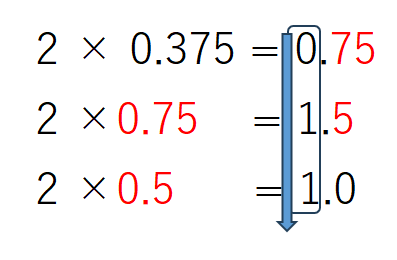
無限小数
10進数の小数点を2進数に変換したときに、無限小数になってしまう場合があります。例えば、10進数0.45が2進数では無限小数です。
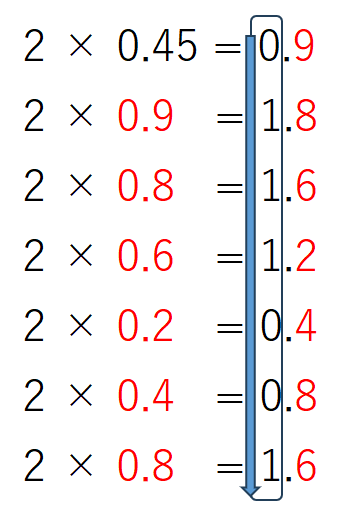
0.01110011001100….と延々と続くことになります。
その他の表現方法
BCD(Binary Coded Decimal:2 進化 10 進)
BCDは2進化10進ともいい、2進数の表し方の1種です。例えば、8桁の2進数00100101は10進数で37ですが、基数の章でやった通り計算を行わないと求められず、ぱっと見てわかるようなものではありません。そこで、少しでもわかりやすく表現しようとしたものがBCDです。
BCDでは4ビットずつ区切り、それぞれを2進数に置き換えます。例えば37であれば0011 0111となります。
パック10進数
パック10進とはBCDを拡張し、末尾の4ビットを符号としたものをいいます。通常1100が正、1101が負になります。